하다보니
오리엔테이션, 기초 코드 작성 요령 1 본문
코딩 테스트는 주어진 문제를 정해진 시간제한과 메모리 제한 내로 해결할 수 있는 능력을 측정하는 테스트이다.
코딩 테스트에서 좋은 성적을 내기 위해서는 배경지식, 문제 해결 능력, 구현력을 두루 갖추고 있어야 한다.
- 우선 배경직식은 다양한 알고리즘, 자료구조, 기타 테크닉 등과 같이 문제를 해결하기 위해 필요한 지식을 의미한다.
- 문제 해결 능력은 배경지식을 지금 당면한 문제에 맞게 잘 변형해서 적용시키는 능력을 의미한다. 전형적인 문제의 풀이뿐 아니라 문제가 마구 변형이 되었을 때에도 이 문제에서 요구하는 알고리즘이 무엇인지 알아내는 능력이 필요하다. 이 부분은 단원의 주제에 맞는 다양한 문제를 접해보면서 조금씩 성장할 능력이다. 이 부분은 스스로의 노력이 많이 필요한 부분.
- 마지막으로 구현력은 본인이 생각한 풀이를 코드로 잘 옮겨낼 수 있는 능력을 의미한다. 실제 코딩테스트를 쳐보면 아예 손도 못 대겠다 하는 상황보다는 분명 풀이는 알겠는데 막상 짜 보니 답이 안 나온다. 혹은 짜다가 꼬이는 경우가 많다. 이러한 상황을 막기 위해선 구현력이 충분해야 하고, 많이 짜보는 것도 중요하지만 입문 단계에서는 내가 맞은 문제를 다른 사람이 어떻게 짰는지를 확인하면서 배울 점을 빠르게 흡수해 좋은 코딩 습관을 가지는 것도 정말 중요하다. 좋은 코드는 흡수하며 자신에게 최적화된 코딩 스타일을 계속 구축해가는 게 좋다.
출처: https://blog.encrypted.gg/921?category=773649
[실전 알고리즘] 0x00강 - 오리엔테이션
안녕하세요, 바킹독입니다. 리뉴얼을 완료해서 다시 강의를 올립니다. 혹시 코딩테스트를 대비하고자 하는 목적으로 검색하다가 이 강좌를 보게 된거라면 지금 이 강좌가 정말 큰 도움이 된다
blog.encrypted.gg
시간 복잡도
컴퓨터는 1초에 대략 3-5억 개 정도의 연산을 처리할 수 있다. 즉 시간제한이 1초라고 하면, 이건 "당신의 프로그램은 3-5억 번의 연산 안에 답을 내고 종료되어야 한다"라는 걸 알려주는 것이다.
시간 복잡도는 입력의 크기와 문제를 해결하는 데 걸리는 시간의 상관관계이다.
빅오 표기법은 주어진 식을 값이 가장 큰 대표 항만 남겨서 나타내는 방법이다. ex) O(n) : 5n+3,2n+10 lgn
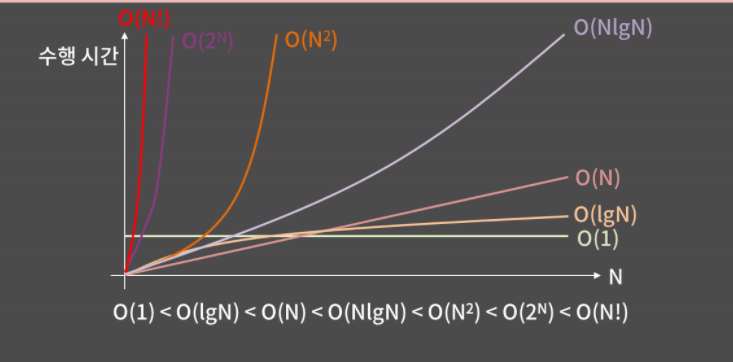
상수 시간인 O(1)이 가장 좋고, 그다음으로는 O(lgN)이고, 이후로 O(N), O(NlgN), O(N²) 등이 있다. O(lg N)은 로그 시간, O(N)은 선형 시간으로 부르고 또 O(lg N)부터 O(N²)까지와 같이 lg N 혹은 N의 거듭제곱끼리의 곱으로 시간 복잡도가 나타내어지면 이를 다항 시간이라고 한다.
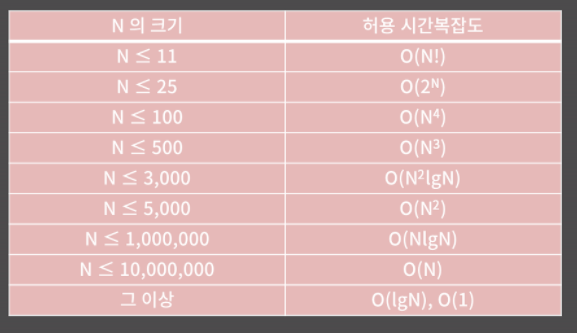
입력의 범위를 보고 문제에서 요구하는 시간 복잡도가 어느 정도인지를 알 수 있다. 입력 N의 크기에 따른 허용 시간 복잡도를 표로 나타낸 게 위의 표이다. 물론 이 기준이 절대적인 것은 아니지만 대략적인 느낌만 가져가면 된다.
앞으로는 주어진 문제를 보고 풀이를 떠올린 후에 무턱대고 바로 그걸 짜는 것이 아니라 내 풀이가 이 문제를 제한 시간 내로 통과할 수 있는지, 즉 내 알고리즘의 시간복잡도가 올바른지를 꼭 생각해봐야 한다.
공간 복잡도
공간 복잡도는 입력의 크기와 문제를 해결하는데 필요한 공간의 상관관계를 의미한다. 코딩테스트에서 대부분의 경우 공간복잡도의 문제보다는 시간복잡도 때문에 문제를 많이 틀리게 된다. 그래서 공간복잡도는 크게 신경을 쓰지 않아도 된다.
대신 문제를 풀 때 메모리 제한이 512MB일 때 int변수를 대략 1.2억 개 정도 선언할 수 있다는 것을 기억해두면 좋다. 이건 int 1개가 4바이트라는 것을 이용해 계산할 수 있다. 이걸 기억해두면 만약 떠올린 풀이가 크기가 5억 인 배열을 필요로 할 때 해당 풀이는 주어진 메모리 제한을 만족하지 못하므로 틀린 풀이라는 것을 빠르게 깨닫고 다른 풀이를 고민할 수 있다.
정수 자료형
char 자료형은 1바이트이다 라는 표현은 1byte는 8bit이니까 char자료형의 값은 8개의 0 혹은 1이 들어가는 칸을 이용해 표현된다는 의미이다. 이 8bit에 2진수 표기로 값이 들어가게 된다. 오른쪽부터 2^0... 2^6을 나타내는 칸인데, unsigned char에서는 제일 왼쪽이 자연스럽게 2^7이지만 char에서는 제일 왼쪽이 독특하게 -2^7이다.
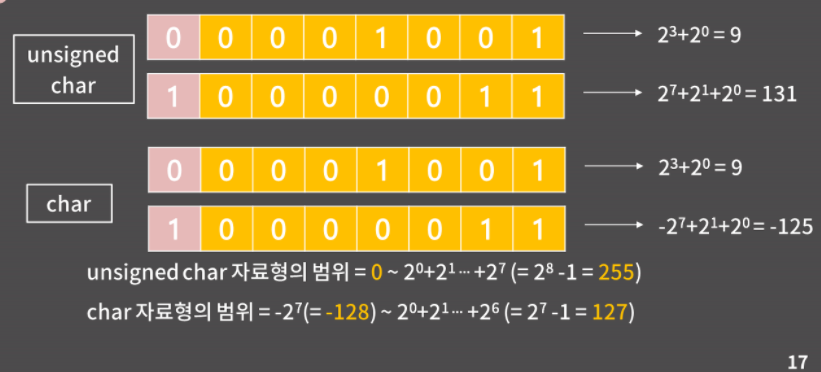
정수 자료형에는 char 말고도 short, int, long long 자료형이 있다. 각각은 2 byte, 4 byte, 8 byte입니다. char의 크기를 계산한 것과 비슷하게 각각이 표현할 수 있는 수의 최댓값을 확인하면 각각 32767, 대략 2.1 ×109(21억), 9.2 ×1018까지 표현할 수 있다.

short는 딱히 쓸 일이 없고 정수를 표현할 때 주로 int나 long long을 쓰는데 int가 long long보다 연산 속도와 메모리 모두 우수하지만 int 자료형이 표현할 수 있는 범위를 넘어서는 수를 저장해야 하면 반드시 long long자료형을 사용해야 한다.
Integer Overflow
정수 값이 증가하면서 허용된 가장 큰 값보다 더 커져서 실제 저장되는 값은 아주 작은 수이거나, 음수인 경우를 말한다. 이것을 막는 방법은 각 자료형의 범위에 맞는 값을 가지게끔 연산을 시키면 된다. 좋은 코딩 습관은 아니긴 한데, 이런 거 저런 거 다 신경 쓰기 싫다 하면 아예 int를 쓰지 않고 전부 long long을 쓰는 것도 하나의 방법이다. 만약 문제에서 unsigned long long 범위를 넘어서는 수를 저장할 것을 요구한다면 string을 활용해서 저장해야 한다. 그리고 그 수로 연산을 해야 하는 문제는 코딩 테스트에 안 나오는 게 정상이긴 한데, 만에 하나 나왔다 치면 그냥 Python을 쓰는 게 C++로 꾸역꾸역 구현하는 것보다 훨씬 편하다.
실수 자료형
실수 자료형으로는 float와 double이 있다. float는 4byte이고 double은 8byte이다. 실수는 2의 음수 거듭제곱을 이용해 임의의 실수를 2진수로 나타낼 수 있다. 실수 저장하는 IEEE-754 format(이 부분은 간단히 이해만 하고 넘어갔다. 다시 보는 것을 추천)
실수의 성질
- 실수의 저장과 연산 과정에서 반드시 오차가 발생할 수밖에 없다. - fraction field를 가지고 각 자료형이 어디까지 정확하게 표현할 수 있는지 보면 float은 유효숫자가 6자리이고 double은 유효숫자가 15자리이다. 이 말은 곧 float은 상대 오차 10^-6까지 안전하고 double은 10^-15까지 안전하다는 소리이다. 오차가 생기는 것 자체는 막을 수가 없지만 오차가 어느 정도인지는 알 수 있다. 두 자료형끼리 차이가 굉장히 크기 때문에 실수 자료형이 필요하면 꼭 float 대신 double을 써야 한다. 실수 자료형은 필연적으로 오차가 있으니 실수 자료형이 필요한 문제면 보통 문제에서 절대/상대 오차를 허용한다는 단서를 준다. 그런데 만약 이런 표현이 없다면 열에 아홉은 실수를 안 쓰고 모든 연산을 정수에서 해결할 수 있는 문제일 것이다.
- double에 long long범위의 정수를 함부로 담으면 안 된다. - double은 유효숫자가 15자리인데 long long은 최대 19자리니까 10^18+1과 10^18을 구분할 수가 없고 그냥 같은 값이 저장된다. 즉, double에 long long 범위의 정수를 담을 경우 오차가 섞인 값이 저장될 수 있다. 다만 int는 최대 21억이기 때문에 double에 담아도 오차가 생기지 않는다.
(여기까지 중에서 double과 float 유효숫자 개수 부분이 아직 이해가 안 갔다. 다시 보면서 공부하기)
- 실수를 비교할 때는 등호를 사용하면 안된다. - 두 실수가 같은지 알고 싶을 때에는 둘의 차이가 아주 작은 값, 대략 10^-12(1e-12로 표현) 이하면 동일하다고 처리를 하는 게 안전하다.
'코테를 위한 알고리즘' 카테고리의 다른 글
| 스택 (0) | 2022.01.11 |
|---|---|
| 연결리스트 (0) | 2022.01.10 |
| 배열 (0) | 2022.01.09 |
| 기초 코드 작성 요령2 (0) | 2022.01.08 |
| 알고리즘 강의 시작 (0) | 2022.01.07 |
